Die klassischen Beispiele für diese Objekte sind die Kepler-Poinsot-Polyeder, bei denen zum Teil auch selbstdurchdringende 5ecke (Pentagramme) verwendet werden.

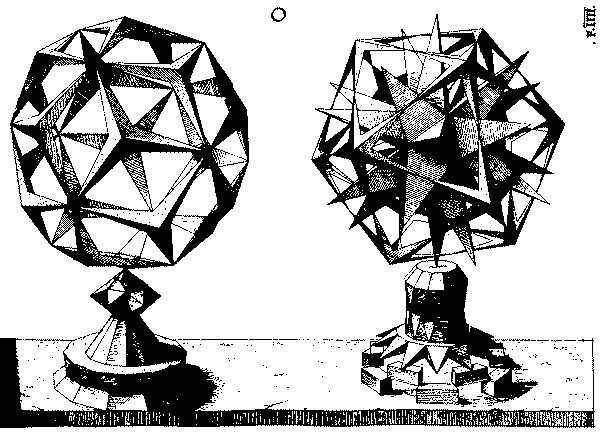
Randbemerkung: Meist werden der kleine und der große Sterndodekaeder Kepler (Harmonices Mundi, 1619) zugeschrieben. Jedoch wurde der kleine Sterndodekaeder bereits ca. 1430 von Paolo Uccello als Mosaik im Eingangsbereich von San Marco, Venedig veröffentlicht. Der große Sternpolyeder wurde anscheinend erstmals von Wenzel Jamnitzer (Perspectiva Corporum Regularium, Nürnberg 1568; Nachdruck – mit einem Nachwort von E. Fiebig – Frankfurt 1972) publiziert.

Bekannt ist auch der Körper, der entsteht, wenn man bei einem Oktaeder drei Quadrate einzieht und dann jedes zweite Dreieck weglässt.
Wegen der Pentagramme in den Kepler-Polyedern lag es nahe, das selbstdurchdringende 8eck (8 gleichlange Seiten, die in 45-Grad-Winkeln aneinanderstoßen) zu verwenden. Mit 6 solchen 8ecken und 8 Dreiecken kann man ein Polyeder bauen; das Bild zeigt ein Modell, in welchem die 8ecke weggelassen sind. Dieser Polyeder wird wiederum zuerst von Kepler im gleichen Abschnitt wie die Sterndodekaeder beschrieben (Harmonices Mundi, 1619). Allerdings hat Kepler die ergänzenden Dreiecke weggelassen und bezeichnet den sich nicht schließenden Rest als Halbkörper (Semisolidus). An der gleichen Stelle beschreibt er auch einen Körper aus Sternzehnecken, ebenfalls ohne die schließenden Fünfecke.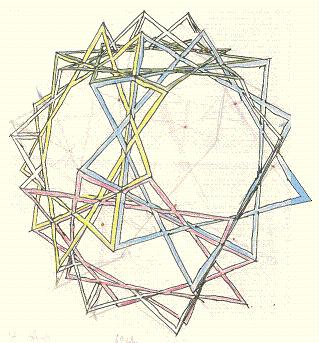

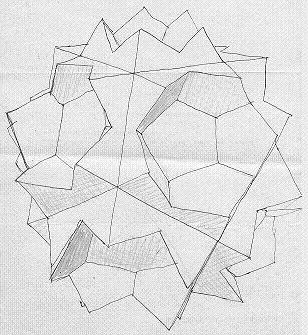
Man kann aber auch den 26-Flächner - den kleinen Rombicubooktaeder - (8 Dreiecke, 18 Quadrate) selbstdurchdringend bauen, indem man Flächenwinkel von 45 Grad (statt 135) anwendet.
Eine weitere Möglichkeit wird hier gezeigt (8 8ecke, 16 Dreiecke):

Immens ist die Anzahl der Möglichkeiten, die sich ergeben, wenn man 5ecke mit Dreiecken kombiniert. Einige sind hier abgebildet:

12 Pentagramme und 30 Sechsecke gehen auch: